
Dynamics

|
Generational Dynamics |
| Forecasting America's Destiny ... and the World's | |
| HOME WEB LOG COUNTRY WIKI COMMENT FORUM DOWNLOADS ABOUT | |
|
These pages contain the complete rough draft manuscript of the new book
Generational Dynamics for Historians,
written by John J. Xenakis.
This text is fully copyrighted. You may copy or print out this
material for your own use, but not for distribution to others.
Comments are invited. Send them to mailto:comments@generationaldynamics.com. |
This chapter has a dual title because we want to do two things in parallel -- develop Chaos Theory as it's applied to Generational Dynamics, and simultaneously develop the nitty-gritty of actual forecasting.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
On the theoretical side, we're going to solve the problem of how cycles and patterns work in history, and we'll show what can and cannot be forecast. On the practical side, we'll summarize some of the specific forecasts that we've been making since 2002 on the web site http://www.GenerationalDynamics.com .
Doing theoretical and practical development in parallel makes sense because the theoretical development has little value unless it has practical value in making predictions and forecasts, and making predictions and forecasts cannot be considered credible unless they're backed up with a solid theory.
The theoretical and the practical have gone together from the beginning. Since 2002, my web site, http://www.GenerationalDynamics.com , has been providing hundreds of forecasts and predictions based on Generational Dynamics. Some of these forecasts have been general, and some have been very specific, many have already come true, none has been proven wrong. This web site has produced results which I would have believed impossible three years ago. And this activity went on as the theory came together.
Incidentally, and this is beside the point, but I believe that this is one of the most significant "real life" examples of Chaos Theory around. Most examples in textbooks are abstract models based on mathematical formulas.
Before getting to the Chaos Theory model, we start with a general description of the different kinds of forecasting. On its own, each of these kinds of forecasting has some value, but most of the power of Generational Dynamics come from combining the different types. With that background, the Chaos Theory model will make a lot more sense.
Short-term forecasting is what everybody uses. To use it, you examine recent previous trends and extrapolate them forward from the present time into the future to make a forecast. This usually works well for growth trends, but not for chaotic trends like weather and politics.
Example: During a November heat wave in New York City, the outside temperature increases every day for two straight weeks. You extrapolate forward and forecast that the temperature will continue to increase in December and January. Obviously, this forecast fails.
This example shows why the kind of political forecasting you want to do fails, and why it HAS to fail.
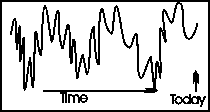 |
The adjoining graph shows what happens. The value being analyzed shows an increase in the period just before "Today." In short-term forecasting, we extrapolate this increase forward, and predict that the value will continue to increase.
A long-term forecast uses a completely different technique, and one that is rarely used by analysts.
The technique is to examine previous trends far into the past to establish long term cycles and patterns, and extrapolate them into long-term trends in the future. To make short-term forecasts, you match current trends to the long-term trends.
Example: In the weather forecasting example, you begin by examining temperature records far into the past, and you discover that the weather is cold every 12 months (in winter). So you conclude that the November heat wave is an anomaly, and you forecast that the temperature is going to fall in December, because you've established long-term patterns with winter coming every year.
This shows why long-term forecasting is more accurate in many cases.
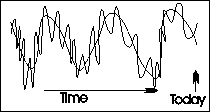 |
The adjoining graph shows what happens. This graph is the same as the preceding one, except that we've added a long-term trend line. Following the long-term trend line allows us to forecast that the value will fall, despite the recent increase.
Example: Based on long-term cyclic trends, Generational Dynamics predicts that there will soon be a major regional war between the Jews and the Arabs in the Mideast. At this writing, in January 2003, the Palestine region appears to be headed for peace. We'll have to wait to see whether the short-term or long-term forecast turns out to be correct.
We're at a unique time in history, about 60 years after the end of World War II, when every country is experiencing the same generational change at the same time: The leaders in government, education, business, labor unions, social organizations and other organizations are people from the generation that lived through WW II (the "Silent Generation"), and they're all disappearing (retiring or dying) all at once, and are being replaced by the people in the generation born after WW II (the "Baby Boomers"). Generational Dynamics gives a very clear picture, on a country by country basis, where each country is going. No standard short-term forecasting technique can produce that result.
Short-term and long-term forecasting have very different characteristics:
By carefully combining the two techniques, we arrive at a prediction that's highly specific, with short or medium term timeframe.
The idea is that the long-term forecasting gives you your destination; then short-term forecasting techniques can be "advised" by the long-term predictions to arrive at a probabilistic short-term result.
We're going to discuss this technique at greater length in the next chapter, on financial forecasts. For example, long-term forecasting predicts that there'll be a new 1930s-style Great Depression sometime in the 2000s and 2010s decades. By following short-term forecasts for things like unemployment rates, inflations rates, and so forth, the time frame can be narrowed significantly. The next chapter will explain this in more detail.
Example: Generational Dynamics predicts that there will be a Clash of Civilizations world war in the next few years, probably sooner than later.
The two World Wars, I and II, have not yet been refought. The only questions are: when will the war begin, and who will be fighting against whom?
In 1945, when WW II ended, we could never have predicted with any certainty that we would be heading for a clash between Western and Muslim civilizations.
Today, Generational Dynamics tells us a great deal about how this world war will begin, and how soon. We'll go over this later, in the section entitled, "The six most dangerous regions in the world."
My last book discussed exponential growth trends in detail, and so here we only summarize that chapter.
Cyclic trends usually apply to values that remain relatively the same over long periods of time. Any increases or decreases are only temporary.
Growth trends apply to values that grow over long periods of time. In particular, when some value in nature grows, it almost always grows at an exponential growth rate, and so we'll restrict our discussion to exponential growth trends.
However, it's a little more complicated: Most populations (including humans) will tend to grow faster than the amount of food available to feed that population. When the population grows to the point where not enough food is available, then a segment of the population is killed -- by famine, by a disease epidemic, or by war. This is the "Malthus Effect" that I discussed in a previous chapter (p. [causes#528]).
For example, how many shoes are manufactured each year? I don't have the figures, but I assume that it's one or two pairs per person around the world, and that's probably been true for centuries. Thus, the number of shoes manufactured each year grows exponentially because the population grows exponentially.
Here's a crucial fact: If there's a temporary perturbation in the size of the population, it will affect the shoe trend. For example, if a world war or an epidemic temporarily causes a 20% drop in the population, then the number of shoes manufactured annually will probably drop about 20% as well.
An example is the power of calculating machines and computers, which has been growing at an exponential rate for over a century, but with no relationship to the population size.
Technological growth is not affected by perturbations in the size of the population. For example, if a world war or epidemic killed 20% of the population, the power of desktop computers would NOT drop 20%. It would stay the same. So the power of desktop computers is unrelated to population. (We'll discuss the exponential growth of computer power again in chapter xxx, p. [next#1265].)
Actually, it wouldn't stay the same: It would continue growing at exactly the same rate. This is the fascinating thing about technological growth -- that it's on a growth path entirely its own, completely independent of population, wars, politics or skirt lengths.
The mysterious thing about technological growth is the steadfastness with which exponential growth trends are maintained for decades or centuries, across wildly varying technologies. We provided numerous examples in my last book, so we'll just give one example here:
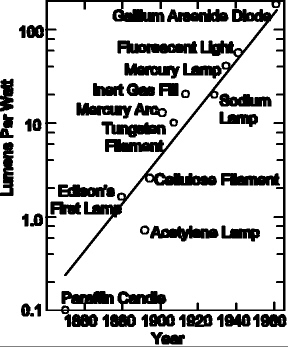 |
Notice in the adjoining graph how new inventions have been improving the efficiency of artificial light sources over time, and how the efficiency has been growing exponentially. Also, notice how each new invention comes at exactly the right time to maintain the steadfast exponential growth.
This graph illustrates how mysterious technological growth is. Why should all these wildly different technologies produce light sources that increase efficiency according to a well-defined predictable growth curve?
Notice also that these technological advances have absolutely nothing to do with population.
This book discusses a number of very different cyclic and growth trends, along with associated forecasting techniques. Generational Dynamics combines all of these trends and techniques to obtain a predictive model that's far more powerful than any single trend or technique used alone.
Here is a summary of the different trends described in this chapter and in other chapters:
Generational Dynamics uses all of these together to get a complete picture. In particular, analyzing short term chaotic events can provide information about how close we are, at any given time, to the final destination predicted by the long-term trends.
Later in this chapter we'll discuss Chaos Theory attractors. Let's introduce the concept now with a couple of examples.
Suppose I ask you to predict the temperature in New York City on January 15 of next year. You might guess something like 30 degrees F (-1 degree C). Why? Because you know it will be winter, and you know that the best guess is a colder temperature. Similarly, you might guess 70 degrees F (21 degrees C) for July 15.
In this example, winter is a long-term cyclic trend forecast, and the day-to-day temperature is a chaotic, random value. Even though the day-to-day temperature is chaotic, it's likely to be close to the trend value determined by the season.
In Chaos Theory, the season trend is called an "attractor," and the day-to-day temperatures are "attracted" to the trend values. This is one way of saying that the daily temperatures are permitted to vary, but are more likely to be close to the trend temperature.
Now let's turn this example around the other way. Suppose you've been imprisoned in a closed room in NYC, and you're going to be freed on January 15. Suppose you have no idea what the date is, but each day you're given only one bit of information: Someone tells you the outside temperature at noon. How do you know when you're getting close to liberation day?
Obviously if the outside temperature is hot, then it must be summer, and so liberation day (January 15) must be very far off. As the temperature grows colder and colder, you can estimate how close you're getting to January 15.
In the first example, we used an attractor trend value (the season) to predict a chaotic value (the daily temperature).
In the second example, we used a chaotic value (the daily temperature) to predict where we were within the trend cycle (the attractor).
In the Generational Dynamics forecasting methodology, the chaotic values and attractor values reinforce each other. In other words, if you know it's winter, then you can predict cold temperatures; if the temperatures are cold, then you can predict it's winter.
Earlier, we said that an ordinary political prediction may have no better than a 50-50 chance of coming true. But if it's the right kind of chaotic political event, and it's "attracted" to the current generational era, then we may be able to say that the political prediction has a 70-30 chance of coming true, or even 90-10.
Thus, in 2002 we were locking up Muslims in jail without charges. This was a drastic change of behavior in the American people, and we've seen nothing of the sort since WW II, when we locked up Japanese without charges. This kind of behavioral shift is characteristic of a generational crisis period, and so I was able to "predict" that we were getting deeper and deeper into such a crisis period.
Once this trend value was established, I was able to "predict" other behaviors typical of crisis periods; for example, I predicted that there would be no antiwar movement of any consequence, since an antiwar movement is not characteristic of crisis periods. Sure enough, through the Afghan war, the Iraq war and its aftermath, and even the Presidential election, there was no antiwar movement to speak of, except for an occasional brief spurt.
As a practical matter, this shows how to use Generational Dynamics to make predictions. WW II ended in 1945, meaning that the next crisis war could begin any time between 1990 and 2030. But by looking at short-term chaotic political values, we can pinpoint where we are in the generational cycle, and thus make very accurate and specific forecasts.
Even with all its restrictions, the forecasting methodology can give you a great deal more information than you might think, mainly because you can firmly predict some negatives.
For example, once you know for certain that there will be a new Arab-Jewish crisis war in the next few years, we can predict with certainty that every peace plan will fail with near certainty. Once we know that Iraq is in an Awakening period, then we can predict with near certainty that there won't be a Sunni-Shi'a civil war. Once you know that a crisis war has begun in earnest in Darfur, then you can predict with certainty that it will run its course, and that the UN will fail to stop it.
Even though these examples are all negative predictions, they still contain a great deal of important information.
So here are some techniques in the forecasting methodology:
 |
There are many further examples and discussions on my web site, and these articles provide more guidance and information on making forecasts and predictions.
Don't expect this to be easy. When I was first getting started, it often took me three or four days of studying various sources just to analyze a single war. As time has gone on, I've been able to proceed much more quickly, but it still requires study of several sources to determine a country's timeline.
Political events are like crack cocaine. Commenting on political events is an obsession, but you're wrong as often as you're right.
Actually, it's easy to get a million political predictions right. All you have to do is make two million predictions. That's all the political forecasting is. You flip a coin to make your prediction, and half the time your prediction turns out right, and you forget about the other half of the time.
Generational Dynamics forecasts are right with nearly 100% certainty, provided that you follow the rules. So what are the rules for commenting on daily news and political events?
Here are some general rules to follow when looking to interpret political events:
With that lengthy introduction to forecasting techniques, we now turn to the use of Chaos Theory to provide the theory support for Generational Dynamics.
Chaos Theory is a new branch of mathematics that was born in the 1960s and has only become seriously studied since the late 1970s.
We give here a brief introduction to Chaos Theory and its sister, Complex Systems Theory (also called Complexity Theory).
If you wish to become a "Generational Dynamics forecasting guru," then you have to have a good feeling about the difference between linear and non-linear systems, chaotic and non-chaotic events. For that reason, you're encouraged to read any of a number of popular books on Chaos Theory that go well beyond this brief introduction.
Chaos Theory is mostly unknown to the public except for one concept, the "Butterfly Effect."
The popular understanding of the Butterfly Effect is as follows:
If a butterfly in China flaps its wings, it can cause a hurricane in America.
This statement of the butterfly effect contains a grain of truth, but it's technically incorrect in important ways. Furthermore, the nature of the technical error is similar to the kinds of errors that journalists, pundits and analysts make on a daily basis in their own forecasting. So it's worthwhile to explore exactly what the butterfly effect really means.
The bottom line is that it is not possible, and will never be possible, to forecast the weather more than a few days in advance. This flies in the face of many people's expectations. People believe that, as time goes on, we'll figure out how to do the science and engineering that will let us predict the weather precisely, as far in advance as we want. But Chaos Theory in general, and the Butterfly Effect in particular, tell us that it's actually mathematically impossible to predict the weather more than a few days in advance.
In fact, Chaos Theory was first conceptualized in the 1960s because of the difficulty in developing software models for weather forecasting.
What causes a hurricane? More prosaically, what causes a sunny day, a cloudy day, or a rainy day? What are the conditions that give rise to each of these weather patterns?
Attempts to develop computer models to address exactly that question ran into an impenetrable roadblock in the form of the following observation:
Suppose you have a computer program that forecasts the weather, based on inputs like air temperature, wind speed, barometric pressure, and so forth. Then you can run your program and get a forecast for the next few days.
Now suppose you rerun the program, but change the inputs only slightly. For example, if you initialized it the first time with a temperature of 39 degrees, then change the temperature to 39.001 degrees. Or change the wind speed from 2 mph to 1.9999 mph.
You might think that such a tiny change in initial conditions would not affect the final weather forecast, but in fact, if your weather forecasting program is realistic, then you'll find that even these tiny changes can have enormous changes in weather forecasts.
So that's why the above statement of the Butterfly Effect is technically incorrect. If a butterfly in China flaps its wings, that doesn't cause a hurricane; rather, it changes the initial conditions enough so that there might be an extra hurricane, or one less hurricane, or a later or earlier hurricane, or it may make a sunny day rainy or a rainy day sunny.
Let's restate the Butterfly Effect in a slightly different manner:
If a butterfly flaps its wings in China, it creates a chain reaction that can change the weather around the world, possibly even resulting in a hurricane in North America.
Here's another way of looking at it: Suppose you could make a second copy of the earth which was identical to the original except for one thing: In one earth, the Chinese butterfly flaps its wings, and in the other earth, the butterfly sits still.
Now, suppose you could watch both earths and see what happens.
What you'd see is that the two earths would not remain identical for long. Thanks to that one tiny initial difference (butterfly flapping wings versus sitting still), the weather on the two earths would quickly begin to differ. The tiny breeze caused by the butterfly in one world would move enough air molecules to make a small breeze somewhere to blow a very tiny bit faster, just enough faster to feed into a stronger breeze somewhere else which, in turn, causes clouds to move in one direction instead of another, which changes a sunny day to a cloudy day, or vice versa.
So the point is this: when the Chinese butterfly flaps its wings, then things change in an unpredictable way.
But is it really unpredictable? Can't a powerful computer compute exactly what would happen?
No, that's impossible, because the computer would have to be too big. True weather forecasting would require simulating the actions of every molecule on the earth, and no computer smaller than the earth itself could perform such a simulation.
There's another reason, too. Computers cannot do precise computations, but can only approximate such things as position and speed, These approximations themselves amount to changes in initial conditions that would have the same explosive effect as the flapping of a butterfly's wings.
So precise weather forecasting is literally impossible, and even predicting the effect of a butterfly flapping its wings in China is also literally impossible.
Again: The butterfly flapping its wings doesn't cause a hurricane; it causes a tiny change in initial conditions which may or may not cause small or large weather changes which are entirely unpredictable.
You might think that the reason that weather forecasting is chaotic is because it's so complex. After all, weather involves the entire earth.
So let's look at a much simpler example, a double pendulum. Spend a few minutes playing around with the double pendulum simulation on the following page: http://www.mathstat.dal.ca/~selinger/lagrange/doublependulum.html (This example requires that your browser support Java.)
As you play with the double pendulum, notice the following:
The double pendulum is a great example because you can actually see chaotic behavior in action. In the case of weather forecasting, you have no way of starting the earth over and over again on the same day to see different weather patterns develop each time, but with the double pendulum simulator, you can do exactly that.
Make sure that you get a feel for why the chaotic behavior double pendulum is important, because understanding that behavior, and applying your understanding, is crucial to understanding the Generational Dynamics forecasting methdology.
Here's a particular experiment you should try: Click on the "Parameters" button to open the control box. Notice the "Total energy (in J)" field reads 289.7. (In physics, a single unit of energy is 1 joule, and so this field indicates 289.7 joules.) Now go back to the moving pendulum, and click on the top center of the square. You'll see that this drags the inner pendulum to the top of the screen, and you'll see that it also changes the value of the total energy field. If you play around with clicking in the square at different times, you'll see that you can either reduce or substantially increase the total energy in the system, to as much as several thousand joules.
Now here's the experiement: Click at the right time so that you get the energy above 800 joules, and watch what happens to the double pendulum. You'll see that it exhibits its usual chaotic behavior at first, but then something very strange happens: After a while, it settles into a large, very non-chaotic circle.
The large circle configuration is call a "cyclical attractor." This exhibits a phenomenon of chaotic systems: That sometimes the elements of the system are "attracted" to an ordered pattern. This is an example of another phenomenon: That sometimes, chaotic systems exhibit an ordered pattern described by such an attractor.
The "attractor" concept is important to our discussion, since later we're going to show that the Generational Dynamics cycles represent a cyclical attractor within the chaos of societal politics.
Here are two more terms you should be familiar with: linear and non-linear systems.
Suppose a basketball is sitting on the rug on your floor, and suppose you push the ball lightly. Then the ball moves a few inches. Now suppose you push the ball hard. Then the ball moves a lot farther.
You and the ball form a "linear system," which means that a small push gets a small reaction, and a large push gets a large reaction. That's what you would expect, right?
But that's not what happens in the double pendulum. Even the tiniest of perturbations completely changes the behavior in a wild, unpredictable way. It's not a linear system.
Neither is the weather. A tiny butterfly's wings can result in major changes.
So a linear system is one in which the size of the reaction to a perturbation is proportional to the size of the perturbation; a non-linear system is one in which the size of the reaction to the perturbation is independent of the size of the perturbation.
A mathematical consequence of this distinction is that a non-linear system cannot be controlled by perturbations. In real-life, this means that political events cannot be controlled by politicians.
Like weather events, political events are completely chaotic. Election polls are like weather forecasts -- they're only good for a few days.
Almost anything has the potential to sway public opinion. A dumb remark by a politician, an affair or a long-forgotten sex scandal, an erratic husband or wife, an endorsement by an outsider, a drunken admission, even a change in the weather -- any of these can turn the public for or against a politician or an issue.
Day to day political events are completely chaotic. A political forecast of almost any kind has less longevity than a weather forecast. And once you accept that, here's a consequence that you may not have thought of: The acts of politicians have little or no impact in the long run. How could they, if any political policy can be easily derailed by the smallest "butterfly"?
It's worth thinking about this for a while, because it's important. All the bitching and moaning about President Clinton's policies and/or President Bush's policies is for nought, since their policies are for nought.
Before I ever heard of generational studies, even before 9/11, I saw a television interview with Supreme Court Chief Justice Rehnquist, and he said one thing so remarkable that I made a note of it. It was on July 4, 2001, and he was asked to describe which of his Court opinions would have the greatest effect on the country and history. He said (paraphrasing): "The opinions that I thought would be most harmful haven't been as harmful as I thought; likewise, the opinions that I thought would be most beneficial haven't been as beneficial as I thought. So the opinions of the Supreme Court perhaps make much less of a difference than we'd like to think they do."
This relates to some points that I made in my last book. If Thomas Edison had never been born, does that mean we'd still be using candles today? No, of course not; someone else would have invented the electric light bulb. If Martin Luther King had never been born, does that mean that the civil rights laws would never have passed? No, of course not. Someone else would have stepped up and led the fight for civil rights.
The same sort of thing is true for crisis wars. Julius Caesar may have started a brief and inconsequential civil war by crossing the Rubicon, but no one person could have started the highly emotional and genocidal civil war in Rwanda in 1994. Assassinations of one kind or another happen all the time, but no one could have known that one particular assassination in 1914 would have triggered World War I. The great crisis wars are huge pulses of energy that ripple through history like tidal waves (tsunamis).
As Leo Tolstoy said in War and Peace,
In historic events, the so-called great men are labels giving names to events, and like labels they have but the smallest connection with the event itself.
Here's one more quote: These are Tony Blair's words when he addressed a joint session of Congress on July 17, 2003, explaining the need for the Iraqi war:
I know it's hard on America. And in some small corner of this vast country, in Nevada or Idaho, these places I've never been but always wanted to go, there's a guy getting on with his life, perfectly happily, minding his own business, saying to you the political leaders of this nation: Why me? Why us? Why America?
And the only answer is: because destiny put you in this place in history, in this moment in time and the task is yours to do.
In each case, the message is the same: Great events are driven by powerful historical forces. History may recognize a particular politician as the agent of change, but the great event will occur irrespective of anything that any politician does or does not do.
Isaac Asimov may well have been one of the most brilliant science fiction writers ever because he was so far ahead of his time, even by science fiction standards. His I, Robot foresaw a world that's not too far off and was portrayed in a recent movie except, of course, the "Three Laws of Robotics" will never be implemented. (See p. [next#1265].)
One of his major works was a three-volume series, Foundation, Foundation and Empire, and Second Foundation.
The premise of these novels is that a genius, Hari Seldon, develops a theory called psychohistory, and is able to use it to predict the future many centuries in advance. Seldon also provides guidance to his followers on how to win wars through cunning, rather than violence. He even predicts the results of elections.
In the story, Seldon's followers succeed with his plan for a couple of centuries, until a freak mutation creates someone called "the Mule." The Mule is a villain who has the ability to control other people's emotions. Because he is so powerful, and because he was unanticipated by Seldon, the Mule alone is able to change history, and to thwart Seldon's psychohistory plan.
In Asimov's vision, the future can be predicted and even controlled, based on mathematical formulas and computer computations. The predictions could be thwarted only by a force that was very large and powerful.
Of course, this was written in the 1940s, well before the wide availability of computers, and well before the discoveries of Chaos Theory. We now know that weather forecasts and political forecasts aren't much good for more than three or four days. We also know that it doesn't take something as powerful as the Mule to change the weather or to change history; it only takes something as small as an ordinary butterfly.
But Asimov's work raises an important question that needs answering: What can you predict, and what can't you predict? If crisis wars are like huge pulses of energy that ripple through history, how do we distinguish the pulse from the chaos? If Asimov had wanted to rewrite the Foundation trilogy with Chaos Theory in mind, what could he have allowed psychohistory to predict (like crisis wars), and what would he have to have left to chance (like election results)?
The discovery in the 1960s that weather forecasting more than a few days in advance is impossible, and always will be impossible, was a shock to mathematicians and scientists alike. That's because weather is a non-linear system, meaning that the tiniest perturbation (like the flapping of a butterfly's wing) can have wild, chaotic effects on the weather that would invalidate any forecasting attempt.
Not being able to forecast weather was bad enough, but they realized that the same conclusion applied to all sorts of other nonlinear systems, things as varied as a dripping faucet, the stock market, politics, gypsy moth populations, the flight of an airplane, and the movement of human heart muscles. If something as simple as the double pendulum (discussed above) was a nonlinear, chaotic system, then almost anything else could be.
As Chaos Theory was developed in the 1970s, a sister theory was born, Complex Systems theory. (Some people call it "Complexity Theory," but I reserve that name for the study of the complexity of computer algorithms.)
If the purpose of Chaos Theory is to find chaotic, nonlinear patterns throughout nature, then the purpose of Complex Systems theory is to bring order out of the chaos.
"But in the 1970s a few scientists in the United States and Europe began to find a way through disorder. They were mathematicians, physicists, biologists, chemists, all seeking connections between different kinds of irregularity. Physiologists found a surprising order in the chaos that develops in the human heart, the prime cause of sudden, unexplained death. Ecologists explored the rise and fall of gypsy moth populations. Economists dug out old stock price data and tried a new kind of analysis. The insights that emerged led directly to the natural world -- the shapes of clouds, the paths of lightning, the microscopic intertwining of blood vessels, the galactic clustering of stars. [James Gleick, Chaos: Making a New Science]
The idea is this: Most chaotic systems of interest have many, many interacting objects, all of which act and interact in a chaotic manner. But suppose that you can step back, and look at the chaotic system at a distance. Very often you see that the innumerable chaotic objects, when viewed from that distance, form patterns that you're unable to see when you're looking at the objects up close.
Think of it this way: If you're scuba diving, and you're underwater, watching the ocean water swirl around you, then the movements of the water molecules around you are totally chaotic. But now, swim to the surface and climb into the boat, and you can see that all those tiny water molecules are forming gentle waves that move across the water's surface. How is that possible? How can a mass of individual water molecules, swirling in individual random, chaotic directions, possibly get organized enough to form waves? That's the kind of question that Complex Systems theory seeks to answer.
And the mathematical answer is called "attractors." You start with thousands or millions or billions of individuals air molecules or water molecules or other objects. Each of the individual objects acts independent in a chaotic matter. However, even though the tiny individual objects act independently, they're still "attracted" to act in a certain way that gives rise to recognizable patterns, such as the waves in the ocean.
The concept of attractors has solved many problems in physics and mathematics in the last few decades.
If you wanted to apply precise physical formulas to individual air or water molecules, you'd soon be lost. In fact, it's been long known that the "three body problem" cannot be solved in a meaningful, closed manner. That is, physicists can give you formulas for two interacting bodies, such as the motion of the earth around the sun. But as soon as you have three objects interacting with each other, then physicists can't give you an answer any more. So hey, if you can't give formulas for three interacting objects, then you won't get answers for millions or billions of interacting objects.
But the mathematics of Complex Systems and attractors solves many of the problems. You can't get formulas for each of the individual air or water molecules, but you can get formulas for the attractors, which describe how the system works as a whole.
We start with fractals because they're so well known, even though fractals don't directly correspond to the Generational Dynamics model we're coming to.
 |
The above graphic illustrates a fractal image. If you go on the internet and type "fractal" into a search engine, you'll have the opportunity to view as many fractal images as you want, many of them quite beautiful.
By definition, a fractal is a complex system that looks the same, no matter how much you magnify it.
If you look at the above image, you'll see that it's composed of repeating patterns. If you could zoom in on one of those patterns, you'll find that the zoomed image is very similar, contains the same patterns, as the original image. If you then zoom in further, you get the same result.
Fractal images represent the attractors in certain types of mathematical systems. Both mathematicians and biologists consider fractals to be of major importance, because the mathematical process that's used to create fractals exactly mirrors the process that nature uses to create most (or perhaps all) of the shapes that appear in nature. The shapes of flowers, leaves, clouds and so forth forth are built up in nature in the same way that fractals are built up according to repetitive application of mathematical formulas.
If you haven't already done so, you should type "fractal" into a search engine, and explore the numerous fractal images on the internet. See for yourself how you can zoom into a fractal and see the same pattern repeat itself in microscopic form.
As we discussed previously, any political system is non-linear and chaotic. Any small "perturbation," can change the results of an election, or of public opinion, within a few days. When pundits say, "A week is an eternity in politics," they're saying that politics is a non-linear system.
From the point of view of Chaos Theory, the principal discovery of Generational Dynamics is that the generational cycle is an attractor for the chaos of political events.
However, it's not an attractor as in fractals, because you can't zoom in and zoom out and see the same pattern. It's more like the ocean wave example, where you can zoom in and see individual water molecules zooming around chaotically, but then zoom out and see them form a cyclical attractor pattern of ocean waves.
When you zoom into the political system, all you see are individuals making individual political decisions every minute of every day. If a politician says something dumb, then the system is perturbed, and people's politics change. If there's an "event," such as a major fire, an earthquake, a terrorist attack, a crime, or even a love affair, how a politician reacts can change many political views.
But the generational cycle is not affected by these perturbations. Crisis wars happen every 70-90 years or so, in every society, and it doesn't matter if there's an earthquake, a crime or an illicit love affair.
You can think of a fractal as a graphical representation of an abstract model of a world represented by certain mathematical formulas. (We are not discussing the mathematical formulas that generate these "worlds," but you can find discussions throughout the internet.)
What's special about the fractal is you can view the fractal in different ways -- zooming in and out, for example, and it always looks the same.
We're now going to discuss a Generational Dynamics abstract model of the world - not just any world generated by a formula, but generated by our real world, and not just the world today, but the world through time.
An abstract mathematical model of the world isn't of much use unless you can prove that the model represents "truth" in the real world. Establishing this "truth" is the purpose of many of the other chapters of this book, showing that crisis wars, awakenings, and generational cycles occur in all regions, societies and nations of the world throughout history. In this chapter, we assume those findings from other chapters.
 |
There is no simple graphical representation of this abstract world, as there is in the case of fractals. However, in order to make the abstract model easier to understand, we'll describe a physical representation of the model, which we call a "magic ball of yarn."
We will examine many different views of the abstract model. However, the abstract model is not a fractal, so the different views won't look the same. That's the power of the model, because each of the different views reveals something different and something new. In this sense, the model will be more like the ocean waves, which look very different when zoomed into the water and zoomed out above the waves.
Let's describe the model through the magic ball of yarn representation:
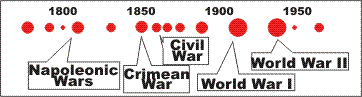 |
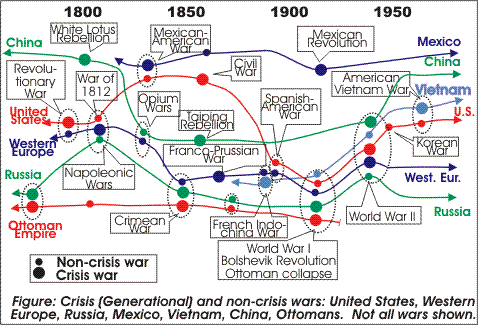
From the chaotic view, you can look around you and see the other wars, looking something like the adjoining graphic. In this view, wars are still chaotically scattered, and there should be no pattern. However, analytical historians have found a pattern - the Kondratiev Cycles (K-Cycles) pattern - that was developed in the 1920s to try to account for wars, including the horrific Great War (WW I). The K-Cycles theory pretty much fell apart in the 1940s, because it didn't predict WW II. Since that time, attempts have been made to revive it. In Chapter xxx (p. [cycles#1175]), we'll discuss another view of the magic ball of yarn model that explains why the K-cycles worked earlier in the millennium, but not later.
 |
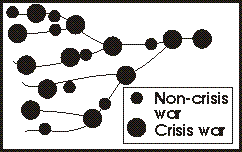
 |
In this view, you examine wars in one society or nation only, and you apply the Generational Dynamics algorithm to each war to determine whether it's a crisis or non-crisis war, as shown in the adjoining diagram. Once the crisis wars have been identified, the crisis wars are shown to have a pattern, as described in other chapters throughout this book.
You can extend the localization view still farther by unraveling several strands of yarn and looking at them at the same time. In this case, you see that different strands merge together and then diverge on occasions.
 |
Although this book focuses on wars, Generational Dynamics establishes many different kinds of patterns, in subjects including politics, culture, technology, economics and international finance, These political, social and cultural values tend to cycle in predictable ways as generations changes, just as wars do.
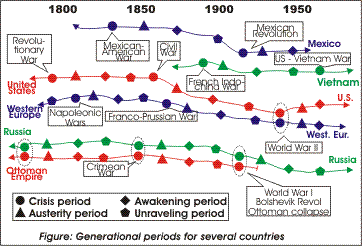 |
In order to identify these additional values, we first have to upgrade the localization view to include all the generational eras, as illustrated in the adjoining diagram. This illustrates a much richer pattern than we saw before.
Along with the four generational eras come all the attributes associated with those eras.
For example, suppose we try to measure the amount of "conflict" in a society over long periods of time. We refer specifically to two kinds of conflict: "genocidal conflict," which happens in crisis wars, and "generational conflict," which happens during awakenings. These are the two kinds of conflict that produce the greatest societal changes.
We might diagram it as follows:
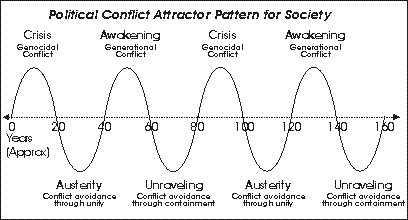 |
This diagram shows what we've been discussing in previous chapters: That conflict levels tend to cycle in predictable ways.
In Chaos Theory there's a concept of a "phase space," which is a graphical representation of the variables which vary cyclically (as opposed to chaotically) in the dynamic systems. In the previous section we talked about the graphic representations of fractals, and those are actually graphs of phase spaces.
Not every aspect of societal life shows a cyclical pattern, as far as I know. For example, the kinds of food we eat may follow an annual seasonal cycle, but they do not follow a generational cycle, to my knowledge.
For the variables that are affected by generational cycles, we turn to the large body of work by William Strauss and Neil Howe in their studies of Anglo-American generational cycles. In their book, The Fourth Turning, they describe each of the four cyclical periods as follows:
Strauss and Howe's brilliant characterizations of the Anglo-American cyclical patterns appear to apply throughout history. Ironically, Strauss and Howe themselves did not believe that the generational cycle paradigm would apply throughout history. They believed that it would apply only to modern times, and then, restricted to modern societies where, "as in America, generations are left free to develop and express their own personalities." (We'll discuss this further in chapter [tftmodel].) But what turns out to be remarkable, as we've shown with our survey of crisis wars throughout history, is that these cyclical patterns always occur, and it makes no difference at all whether or not "generations are left free to develop and express their own personalities."
In fact, nothing makes any difference. The same things happen in democracies, republics, fascist dictatorships, or communist dictatorships. It happens in Muslim societies, Christian societies, Buddhist societies, and pagan societies. It happens to people with white skins, yellow skins, brown skins and black skins. It happens with vegetarians and meat eaters.
It makes no difference if a society or nation is technologically advanced or backwards, moral or immoral, rich or poor, religious or atheist, artistically enlightened or poetically challenged. Every 70-90 years that society or nation tries to obliterate another society or nation.
And crisis wars begin in all different kinds of ways. Sometimes there's an obvious agent of war, such as Adolf Hitler or Napoleon Bonaparte or Chief Shaka of the Zulus or King Louis XIV of France. In other cases, wars begin in a way that resembles spontaneous combustion, as in the Rwanda genocide of 1994, the assassination that sparked WW I, China's Taiping Rebellion, or the Reign or Terror that grew out of the French Revolution.
Midway between crisis wars there are Awakening eras, characterized by generational conflict. There are always riots and demonstrations, usually by students against aging politicians, with China's 1989 Tienanmen Square demonstration being one of the most famous of recent times. There's almost always an element of spirituality: England's Puritan awakening of the early 1600s, America's anti-Puritan awakening thirty years later, America's Great Awakening of the 1730s, America's "God is Dead" awakening in the 1960s, or the Sunni versus Shi'a theme in Iraq today. Gender issues (or "women's issues") often become paramount in awakenings, whether it's "women's lib" in America's 1960s, showing the Can-Can in 1890s Paris, or Caesar making Cleopatra ruler of Egypt during Rome's awakening period in the 40s BC. Public concern for minorities appears to increase during awakenings, and labor turmoil seems to increase.
So the political issues that give rise to the four generational eras vary from society to society, and from century to century. But the generational cycles occur nonetheless, always in the same order, and always with the same results.
That's why the variables we've discussed -- riots, genocidal conflict, generational conflict, spirituality, gender issues, concern for minorities, and labor turmoil -- form the "phase space" variables and the attractors that bring order out of the chaos of day-to-day societal politics.
One stock market commentator defines a bear market as a time when "investors are looking for reasons to sell," and a bull market as a time when "investors are looking for reasons to buy."
This is a great characterization, because it zeroes in on the true meaning of an attractor.
During an unraveling era, a country looks for compromise and containment when problems occur; during a crisis period, a country looks for confrontation.
But neither of those characterizations is monolithic. It doesn't mean that everyone wants to compromise during an unraveling era, or that everyone wants to confront during a crisis period.
It means that during an unraveling period, people "look for reasons to compromise," but during a crisis period, people "look for reasons to confront."
There are always plenty of reasons for investors to buy or sell stocks, and there are always plenty of reasons for the public to favor compromise or confrontation.
But during one period or the other, the investors or public "look for reasons" to go in one direction or the other.
Here's one more way of looking at it.
Imagine that you're rolling a ball inside a round bowl or basin. The ball will roll around the sides and eventually settle at the bottom of the basin. If you then perturb the ball or push the ball or smack the ball, it will roll around some more, but once again it will settle on the bottom. Thus, the ball is "attracted" to the bottom of the bowl.
Chaos Theory refers to the concept of "basins of attraction." The idea is that a chaotic system can settle down into a cyclic pattern defined by a cyclic attractor. But in order to be able to claim that a pattern is truly an attractor, then you have to be able to prove that it's like a ball in a basin: If you perturb the system while it's cycling through the pattern, then it had better return to the pattern again.
Behavior in a basin of attraction is the opposite of chaotic behavior. When you perturb an object behaving chaotically, then the perturbation changes the object's behavior in a wild, unpredictable manner.
But if you perturb an object in a basin of attraction, then the object returns to the same behavior as before the perturbation, just as a perturbed ball in a basin returns to the bottom of the basin.
In fact, in chapter xxxx we already showed that the generational paradigm is extremely robust, and returns to the pattern even if perturbed. This is shown through the following diagram:
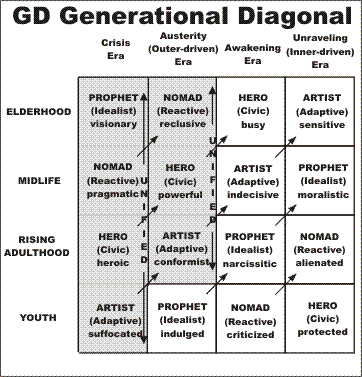 |
This diagram shows how generations change through the entire generational cycle. The darkened squares are the ones that show that the generational paradigm is indeed in a "basin of attraction."
Suppose you perturb the society with an unexpected crisis war, literally putting the society in mortal danger, so that the society is in the left-hand column with the wrong generations in place. However, at the time of such a crisis, all generations must unite for survival, so generational differences are muted. This unity continues through the Austerity period, and only comes apart during the political conflicts of the Awakening period. But whatever their generational archetype when the entered the Crisis period, they'll become heroes for having fought in the crisis war. The youth generation will be Artists for having grown up during a crisis war. By the Awakening period, the other two generations will have disappeared (retired or died).
This shows that if a perturbation occurs in a society, even a huge perturbation like an unexpected crisis war, then the generational change pattern corrects itself very quickly -- within just two generations. This shows clearly how powerful and robust the generational pattern is.
In order to claim that generational cycles form a strong cyclic attractor in the sense of Chaos Theory, we have to show their robustness, meaning that the cycles continue even when perturbed.
One of the most interesting examples of the robustness of the generational paradigm is the Puritan Flip, described on p. [tftmodel#2402]. Briefly, it happened as follows:
England went through the Puritan Awakening period beginning in 1604, when James VI ascended to the throne, sparking first widespread opposition to Anglican Church. By 1606, a separatist church had been formed by the Puritans, and they were so harassed that they were forced to flee to Holland. This was the group of Pilgrims that landed at Plymouth Rock in 1620.
Intuitively, one would expect the Pilgrims to retain the same generational archetypes in the colonies that they'd had in England, but remarkably they didn't. Instead, something quite different happened, a kind of "awakening inversion" that flipped the colonial turnings around from what they were in England.
The migration of Englishmen to colonies was not unlike a crisis period in the following sense: Petty political and personal differences had to be put aside, and all generations had to unite in order to survive in the new land. Thus, during the period 1610-30, while the Puritan awakening was going on in England, the Puritans who migrated to the colonies were actually going through a kind of Crisis period, before things settled down into an Austerity period.
During an Austerity period, everyone unites to impose a structure on society to protect it. The kids born during the Austerity period rebel against this structure, and that's what causes the Awakening period. In the case of the colonies, the structure was based on Puritan principles, and when the Awakening era arrived, it was to rebel against Puritanism.
So, when the Pilgrims rebelled against the Anglican Church, Puritanism was the "new thing," the "cool thing," the "hot thing" for their time. When they migrated to the colonies, the kids grew into obnoxious Puritan adults, and their kids rebelled against them. Thus, the migration was a kind of pseudo-crisis that forced the unification of the generations, but the kids born after the migration had the same sort of generation gap that appears in all awakenings. So, by the 1640s, when England was having a violent, genocidal crisis civil war, the colonies were going through an awakening, with kids rebelling against old, stodgy Puritanism. This put the colonies onto an entirely different schedule, two generations out of phase with their parents in England. New England's next crisis war came on schedule with King Philip's war, beginning in 1675. America's timeline didn't merge again with England's timeline until World War II.
The Puritan Flip is a great illustration of the robustness of the generational paradigm. In particular, it shows that if there's a perturbation, then the standard generational pattern is fully reestablished within two generations following the next crisis war.
How is it possible to go from a chaotic view to an ordered view? How can a system consisting of thousands or millions or billions of individual objects, each one acting chaotically, possibly "work" together well enough to exhibit any sort of pattern? More specifically, how does an "attractor" work, anyway?
In order for the individual objects, each acting chaotically, to behave collectively so that the system as a whole is ordered, some sort of synchronization must occur. This is usually called either "phase locking" or "entrainment."
"Entrainment" is the more restrictive form of synchronization. It occurs when the individual objects we're talking about all continue their behavior as before, but slowly "train" one another to act together.
There are examples of entrainment throughout nature:
These are simple examples of entrainment that occur throughout nature. In each case, you have groups of individuals that normally act and interact in a chaotic manner, but they develop ordered behavior because they entrain each other to synchronize their independent actions so that they act together.
Entrainment is an important kind of phase locking, though it's not the only kind. It's worth looking at these examples because they will provide additional insight into the working of the generational model we're describing. Phase locking will also become an important part of the generational model when we add Kondratiev cycles to it in Chapter xxx (p. [cycles#1175]).
If you don't yet completely understand attractors, entrainment and phase locking, then it may help to relate to a common economic concept: the law of supply and demand.
Consider the microeconomics Law of Supply and Demand for determining prices in a free market. According to this law, prices decrease as supply of a product increases, and prices increase as demand for the product increases. The prices reaches an equilibrium equal to the marginal cost of providing (manufacturing and marketing) the product.
How is this equilibrium reached in practice? It's a kind of phase locking mechanism.
Imagine consumers buying loaves of bread from bakers all over the country, and it's "in the old days," so the buyer and baker have to agree on a price. As are all such actions, these are chaotic events, occurring at unpredictable times, with sales at unpredictable prices. And yet, all the price transactions quickly reach an equilibrium price that everyone pays.
The phase locking mechanism that provides that equilibrium is "word of mouth price comparisons." Consumers do price comparisons, and tell each other about them. Newspapers print stories about prices, and tv does news segments. Sometimes consumers might even stage "bread strikes" to convince vendors to bring prices down.
Stores and distributors also compare prices among their suppliers, and choose among the ones with the lowest prices for equivalent products.
Interestingly, manufacturers are not allowed compare prices with one another in order to make the prices as high as possible, since they're forbidden from doing so by antitrust laws. So phase locking occurs entirely at the consumer end, not at the manufacturing end.
Whenever an economic equilibrium must be reached, there is probably a phase locking mechanism like the one summarized above.
Relating this to Chaos Theory, the equilibrium price becomes the attractor. It's a robust, stable equilibrium, because if there's a perturbation away from the equilibrium price, then the price will return to the equilibrium price quickly. For example, if someone tries to charge too much, he'll quickly go out of business, as his competition undersells him.
The equilibrium price is a "point attractor" in terms of Chaos Theory. But now let's extend this example through time, and assume that bread prices tend to be lower in fall, just after the wheat harvests, than they are in the spring.
Then the equilibrium price will show a cyclic, seasonal pattern. This would be called a "cyclic attractor."
We'll conclude this discussion with one more related example: The spread of technology.
When new technology is developed or invented in one region, then it's quickly copied from region to region, so that all regions are pretty much synchronized with respect to having the latest technology.
Of course, "having the technology" is different from "using the technology." The latter depends on having the appropriate infrastructure to take advantage of new technologies when they come along.
This relates to one theory of non-crisis wars. Generational Dynamics explains crisis wars, but provides no real guidance for non-crisis wars, which are usually purely political. One possible generator of mid-cycle wars is the development of new technology. If one country has the infrastructure to use the new technology quickly, then that country may decide to take advantage of the situation to declare war on another country, without the necessary infrastructure.
Technology is a good example of phase locking that doesn't depend on oscillations, and doesn't depend on entrainment. Technology exhibits exponential growth rather than cyclic growth, but the usage of technology appears to follow a 40-50 year cyclic pattern. This is one of the theories that explain Kondratiev cycles (p. [cycles#1175]).
Generational systems use a completely different kind of phase locking from the kinds we've just described. In the examples so far, there were innumerable individuals performing chaotic events which became synchronized in some way because of some kind of "sharing" between the individuals.
Generational systems are quite different because individual people don't "oscillate" in the same way that flashing fireflies and chirping crickets do. In fact, the decades-long time frames for generational patterns do not lend themselves to any of the phase-locking examples we've described.
In generational systems, phase locking occurs because new people are added to the system at roughly the same time (birth of a generation) and leave the system (retire or die) at approximately the same time. Patterns occur because people in the same generation share characteristics, and it's these characteristics that define the ordered patterns.
The crisis wars provide the anchor point to the pattern. Phase locking occurs during crisis periods because all generations unify for the survival of the society or nation, or its way of life. Once the crisis is over, the generation born after the war rebels against the generation of heroes that fought in the war (during the "awakening"), so the phases are locked again into the pattern.
It's remarkable, really, that this pattern occurs over and over: crisis period, austerity, awakening, unraveling, crisis, austerity, awakening, unraveling, and on and on.
And, yes, occasionally the generational pattern is perturbed by an unexpected war, or by an unexpectedly long unraveling period without a war. But as soon as a new crisis war occurs -- and it always does, because there's always genocidal competition for food, land, and other resources -- then the new crisis war synchronizes the generations again and restarts the generational cycle.
The remainder of this chapter is devoted to giving a lengthy example of various techniques in Generational Dynamics forecasting.
Anyone reading my web site realizes that Generational Dynamics predicts that we're heading for a "clash of civilizations" world war in the next few years. We will be using probabilistic forecasting to determine the probability of a major new world war during 2005. (This analysis should be considered correct as of the end of 2004.)
There are six regions in the world (Palestine-Israel, Russia-Caucasis, India-Pakistan, China-Taiwan, Korea-Japan, Western Europe) that are all becoming so tense that a spark could ignite a war in any of them, and a war in any of them would probably trigger a "clash of civilizations" world war.
For almost 20 years, historians have been discussing the possibility of a new major world war, a "clash of civilizations" between Western civilization and Muslim civilization, with well over a billion people on each side.
The concept was popularized by Harvard professor Samuel P. Huntington in his 1996 book, The Clash of Civilizations and the Remaking of World Order. In his book, he analyzed Muslim civilizations around the world and discovered, in particular, that population growth was much higher in Muslim than in Western countries, creating a "youth bulge" which, he predicted, will lead to the clash by the 2010 time frame.
Today, thanks to Generational Dynamics, we can get a pretty firm idea of the likeliest scenarios that will lead to the "clash of civilizations" war.
The six regions that we've selected are the most likely to trigger a major war mainly because a war in any of these reasons will quickly force America to join the war on one side or the other, usually because of existing treaties. Furthermore, each of these regions is in a "generational crisis" period, which means that even a small regional war in one of these regions is likely to spiral out of control into a very big war.
Here are the six regions:
The above regions are all dangerous for the obvious reasons given, but those regions are particularly important for another reason: They're all in a "generational crisis" period.
We're at a unique time in history because 60 years have passed since the end of World War II, and all the nations who fought in World War II are now making rapid generational changes, all at the same time. In each nation, all the people who have personal memories of the genocidal horrors of WW II are all disappearing (retiring or dying), all at once, and history tells us that that's when the next world war is likely to begin.
From the point of view of Generational Dynamics, different nations and regions throughout history have been on different "timelines," which indicate when major genocidal crisis wars occur. In the last century, most of these distinct timelines have merged into two major ones: A World War II timeline, and a World War I timeline. Of the six regions above, Russia-Caucasus is on the World War I timeline, and the others are on the World War II timeline.
About 55-60 years after one crisis war ends, the last generation of people who have personal memories of the genocidal horrors of the preceding crisis war, the country enters a "generational crisis" period. This appears as a substantial change in attitudes in the public in general. We've already begun to see this in America, with the surprising and unexpected rise of "moral values" as a factor in the last election. Whenever any country enters a generational crisis period, public opinions continue to harden until a new crisis war breaks out.
Opinions and attitudes today have been hardening in each of the six regions we're discussing. Whether it's Palestinians versus Jews, or Taiwan versus Beijing in China, or the Beslan school massacre in the Caucasus, or the sudden, rapid hostility between Christians and Muslims in the Netherlands, opinions are hardening rapidly in these regions around the world.
In the previous section, we gave some examples of specific forecasts, but they were all negative (there will NOT be a civil war in Iraq).
Positive forecasts are like the saying, "A watched pot never boils." You know that the water will boil some time, but you don't know when. So you can say that there'll be a major Arab-Jew crisis war in the next few years, but you can't say exactly when.
However, it should be possible to give probabilistic forecasts.
We start with this table, which also appears in an earlier chapter. It shows the number of crisis wars that began in a specified number after the end of the previous crisis war:
Fraction
# years of total
------- --------
0- 40 0%
41- 49 11%
50- 59 33%
60- 69 25%
70- 79 16%
80- 89 4%
90- 99 6%
100-117 5%
This estimate is based on principles of Generational Dynamics which itself is based on studying repeating patterns throughout history.
I took the data that went into this table, I did some smoothing and made some computations involving conditional probabilities, and came up with the following table, which gives the probability of a new crisis war beginning in that year (given that it hasn't already begun in a previous year):
|---|------|------|------|------|------|------|------|------|------|------| | Yr| +0 | +1 | +2 | +3 | +4 | +5 | +6 | +7 | +8 | +9 | |---|------|------|------|------|------|------|------|------|------|------| | 40| 0.00%| 0.11%| 0.23%| 0.34%| 0.46%| 0.58%| 0.70%| 0.85%| 0.99%| 1.15%| | 50| 1.31%| 1.47%| 1.68%| 1.90%| 2.13%| 2.37%| 2.83%| 3.33%| 4.31%| 4.31%| | 60| 4.32%| 4.32%| 4.32%| 4.32%| 4.33%| 4.33%| 4.33%| 4.33%| 4.34%| 4.34%| | 70| 4.34%| 4.34%| 4.35%| 4.35%| 4.35%| 4.35%| 4.36%| 4.36%| 4.36%| 4.36%| | 80| 4.37%| 4.37%| 4.37%| 4.37%| 4.38%| 4.38%| 4.38%| 4.39%| 4.39%| 4.39%| | 90| 4.39%| 4.40%| 4.53%| 4.68%| 4.84%| 5.01%| 5.20%| 5.41%| 5.63%| 5.87%| |100| 6.14%| 6.44%| 6.77%| 7.14%| 7.56%| 8.04%| 8.60%| 9.24%|10.00%|10.91%| |110|12.02%|13.40%|15.18%|17.54%|20.85%|25.00%|25.00%|25.00%|25.00%|25.00%| |---|------|------|------|------|------|------|------|------|------|------|
Thus, America's last crisis war ended in 1945, which is 60 years ago, so the probability of a new crisis war beginning in 2005 is 4.32%.
So, we can't predict when America's next crisis war will begin, but we can use just one fact -- the time since the end of the last crisis war -- to determine that the probability that a new crisis war for America will begin in 2005 is 4.32%.
Now, let's continue with this exploration by using some additional information.
As we've said, timelines have been merging throughout history, creating two major timelines in the 20th century, the WW I timeline and the WW II timeline.
Today, we're at a unique time in history when even the East European and West European timelines are merging into a "clash of civilizations" world war, with the West on one side and the Muslim civilization on the other.
This brings us back to the six dangerous regions that we began this article with:
Each of these regions had separate crisis wars in the 20th century, with the first five on the WW II timeline, and the last (Russia and the Caucasus) on the WW I timeline.
As an aside, note that some other crisis wars on the WW I timeline have already completed; these include the Iran/Iraq war of the 1980s, the Lebanon/Syria war starting in 1976, the Turkey/PKK-Kurd war of 1984-2000 and the Balkans wars of the 1990s. That's why most of the coming conflict is on the WW II timeline, with a sprinking of the WW I timeline merged in.
However, the biggest of the WW I timeline wars has yet to be refought: the Russian revolution and the massive civil wars of the 1920s.
Now here's the assumption that I'm making: If a crisis war breaks out in any one of the above six regions, then it won't remain a regional crisis war for long; instead, it will end up engulfing America and all six regions, ending up as a new world war.
Thus, what we need to do is compute the probablity that a crisis war will break out in at least one of the above six regions.
In order to do that, we have to make one more assumption: That before the world war begins, the probability of a crisis war in any one of those six regions is independent of the probability of a crisis war in any of the others. This is in fact probably true, since each of the previous crisis wars was a separate war.
This assumption will allow us to use the independent probability rule to make computations.
So the first thing we need to do is compute the probability of a crisis war in each of the six regions. To do this, we used the same table of probabilities that we used above to compute the 4.32% value for America.
So, it's now appropriate we ask: What's the probability that at least one of these regions will have a crisis war in 2005?
For that, we need to first compute the probability P of a crisis war beginning in 2005 for each region separately, where Y is the year of the last crisis war:
| Region | End of last crisis war | P for 2005 |
|---|---|---|
| World War I timeline | ||
| Russia-Caucasus | Russian revolution, civil war between Lenin and Trotsky,
Y=1928, 75 years ago | P=4.36% |
| World War II timeline | ||
| Western Europe-Pacific | World War II,
Y=1945, 50 years ago | P=4.32% |
| Palestine-Israel | War between Arabs and Jews,
Y=1949, 46 years ago | P=2.83% |
| India-Pakistan | Muslim-Hindu conflict, World War II.
Y=1945, 50 years ago | P=4.32% |
| China-Taiwan | Civil war between Mao
Zedong and Chiang Kai-shek Y=1949, 46 years ago | P=2.83% |
| Korea-Japan | Japanese occupation of China, World War II, partitioning of
Korea. Y=1946, 49 years ago | P=4.31% |
So now we use the rules of independent events to compute the probability of a crisis war in 2005 in at least one of the above regions is:
1 - (1-.0432)*(1-.0283)*(1-.0432)*(1-.0436)
*(1-.0283)*(1-.0431)
= .2089 = 20.89% ;
So, according to this calculation, the probability of a new crisis war in at least one of these regions in 2005 is about 21%, or a little more than 1 in 5. If it doesn't happen in 2005, then the probability will be a little higher in 2006. Here are the probabilities for each of the next few years:
2005 20.89%
2006 21.71%
2007 23.29%
2008 23.30%
2009 23.33%
2010 23.34%
This table gives the probability of a world war involving America starting in each year, given that a world war has not begun in a previous year, and provided that the original assumptions (that a regional war in one of these regions will lead to a world war) still hold.
However, this 21% result assumes you know nothing else about the countries involved, other than the one fact - how long it's been since the last crisis war. My personal feeling is that the international situation has deteriorated significantly just in the last year, and the probability of a major crisis in 2005 is definitely higher in 2005 than it was in 2004. I note in particular the following:
If I had produced a list like this at the end of 2003, the list would have been shorter, with fewer specific items. That's why I say that things have gotten significantly worse in the last year.
If "nothing happens" in 2005, then my expectation is that the above list (with the exception of the first item) will only get longer for 2006.
We've used the example of the six most dangerous regions in the world today as a framework to describe the theory behind Generational Dynamics and the Forecasting Methodology.
We've used this presentation to estimate the likelihood of a major "clash of civilizations" world war in the next few years. We're at a unique time in history where all the nations that fought in World War II are simulataneously entering a new generational crisis period, and so the likelihood of a new world war is increasingly high. We used probabilistic forecasting, under certain named assumptions, to estimate that there is approximately a one in five chance that the war will begin in 2005.