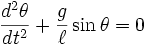Actually, Justin is right, and I'm going to have to concede the point at least where he is concerned.

It's too bad, because instead of libertarian principles, it means he's a die-hard skeptic out of sheer contrariness, and thus probably a hopeless case.

Originally Posted by Brian Rush

It's too bad, because instead of libertarian principles, it means he's a die-hard skeptic out of sheer contrariness, and thus probably a hopeless case.

I've been found out

Of course, science -- as you more or less told Rani just above:

...as a practical matter, we can't afford the conservatism that's inherent in good science.

is an endeavor for the skeptical.

Besides, as Twain said, any time you find yourself on the same side as the majority is a good time to take a step back and reconsider your position.

Originally Posted by Justin '77

First prize in the Shooting Right Past The Point Contest goes to the 'bert!

In fact, I'm not even terribly sure just where you ended up. Much less how you got there from my attempt to summarize the fundamental goal of any who might feel compelled to fight against AGW. Maybe is just as valid for this one...

In your discussion with Brian and in the post I cited you made this assumption. You imply that if people were certain that their actions did cause harm then the harm could be redressed by individual actions. But not such certainty exists. Obviously, if we are debating the reality of the AGW theory, we cannot assume it is correct. Do you understand this?

Brian asked to argue with this assumption, which leaves science out of it and lets you go into philosophy, where there are no right answers.

But in our discussion we were still debating where or not AGW has been established. Its seems pointless to discuss what should be done, if it isn't real. So why assume that it's reality has been established?

You implied that your faith tradition is open to accepting AGW as reality. That is, you deny you are like the creationist contemplating evolution.

But your actual discussion of AGW's reality doesn't support this assertion. You haven't denied that warming is actually occurring. You haven't denied that humans put a lot of CO2 is not the air and that some of it stays there, resulting in rising levels over time. You haven't denied that CO2 is a greenhouse gas and so will (all else being equal) produce warming. So far you have yielded a lot of ground. Of course denying empirical reality would put you squarely in the creationist category.

You try to suggest that is somehow unreasonable for human factors to be larger than natural variations. This is really irrelevant, but you don't go anywhere with the argument so its a non issue.

All of the empirical evidence says that global temperature in the last decade are higher than any in the past millennium. CO2 levels are much higher than any before 1900 going back many thousands of years.

You seem to acknowledge that something is going on with climate by trying to roll out the cosmic ray model as an alternate explanation for warming. The way you did so was to obfuscate the issue with a red herring "galactic topology". Resorting to tricks is usually a good sign of a poor argument.

Skeptics like to point out that "solar activity" has been at the highest levels in a millennium over the 20th century so as to try to discount the empirical fact that in recent years, temperature and CO2 has been higher than it ever has been in at least 1000 years. Yet when it was shown that the high solar activity reached this level in the 1950's and has been flat since there has been no comment from you.

You seem impervious to evidence, like like a creationist wrt to evolution.

Originally Posted by Justin '77

Of course, science -- as you more or less told Rani just above:is an endeavor for the skeptical.

Yes, but there's where the difference between standards of proof in different language-games comes into play. There's a dialogue about global warming within academic science, and then there's another dialogue about global warming OUTSIDE academic science for political purposes. Most of the global warming skeptics in print and on the Net are taking part in the latter dialogue, not the former one. The scientific argument, properly so called, is restricted to peer-reviewed publications and talks inside academia.

The models we have today are not as good as the models we will have ten years from now. It's possible -- although increasingly unlikely -- that the models ten years from now will show that anthropogenic factors aren't the main cause of the warming we are seeing. But if we wait ten years for that increased certainty, we will not take action that -- unless that unlikely possibility comes off -- we need to take before then. And, ten years from now, it will still be possible to argue the same thing, and call for waiting ten more years. There will never be certainty. Never.

In terms of politics, we have to reach a point where we say, "OK, good enough. Let's roll." And then we leave science to fill in the details as we roll, and correct our course accordingly one step at a time.

Besides, as Twain said, any time you find yourself on the same side as the majority is a good time to take a step back and reconsider your position.

Originally Posted by Mikebert

You seem impervious to evidence, like like a creationist wrt to evolution.

I guess at the end it comes down to what case exactly you expect the evidence that you offer to make for you.

Does the evidence appear to correlate CO2 levels with global temperature? At least weakly, yes. Does experimental evidence indicate that there is a mechanism whereby CO2 could act as a greenhouse gas? Yes. Does evidence indicate that human activities have dumped increasing amounts of CO2 into the atmosphere at least over the second half of the last century? Yes.

Does the accumulated evidence do more than suggest -- at best -- that human CO2-producing activity may have some warming impact on the global climate? No.

The problem isn't that someone else has a mechanism which explains where the warming is coming from (which appears to be what you are looking for from the galactic topography discussion); it is that the anthropogenic CO2 explanation is far from rigidly exclusive. The models are fundamentally based on an assumption that a chaotic, mega-multi-input system can be understood on the basis of a small number of inputs over a vanishingly small time interval. Other inputs -- which both undeniably exist and are undeniably not tracked at present -- have impact, and as the last thirty-some-odd years of study of chaotic systems should have made clear by now to anyone, even small inputs can cause effects of all manner of scope.

Engineers make all sorts of boundary assumptions in their work; but those boundary assumptions are generally justified by either empirical evidence or by actually resolving the fundamental equations at least the one time to demonstrate that the assumed-out components are actually not critical at the scale of resolution and input being considered. This has not been done for the AGW hypothesis. Instead, AGW True Believers keep coming back to consensus. Which is one of those arguments which, the more times one hears it, begins to have a somewhat negative return...

Originally Posted by Justin '77

IOther inputs -- which both undeniably exist and are undeniably not tracked at present -- have impact, and as the last thirty-some-odd years of study of chaotic systems should have made clear by now to anyone, even small inputs can cause effects of all manner of scope.

Is the climate a chaotic system or a linear one? Weather is certainly a chaotic system, but climate is not weather. If we are dealing with a linear system, then small variations in initial conditions will produce only small variations in outcome.

Former Fox Host Helps CNN Promote Glenn Beck’s Anti-Global Warming Agenda

Last night, CNN’s right-wing pundit Glenn Beck — who has a history of making flagrantly false and offensive statements — aired a documentary on global warming entitled “Exposed: The Climate of Fear.” Beck concluded, “Al Gore’s version of climate change has no longer become science. It’s dogma. And if you question it, you are a heretic. … The debate is not over. I have a feeling it’s just beginning.”

Beck’s program mentioned Gore 32 times. As much as Beck would like to turn climate change into a personal attack, the scientific judgments of Gore are the consensus view of the world’s leading scientists. The IPCC — “history’s most definitive statement of scientific consensus on climate change” — recently released its main findings, stating global warming is “unequivocal” and human activity is the main driver, “very likely” causing most of the rise in temperatures since 1950.

This morning, CNN continued to help peddle Beck’s agenda, giving him a platform on its morning show to help spread his uninformed views. Host Kiran Chetry, formerly an anchor of Fox and Friends and recently hired by CNN, conducted an interview worthy of Fox News, tossing softballs and teeing up some of Beck’s false claims. A sampling of her questions:

– [I]t appears that most people think that global warming is caused by man. And when you raise a different opinion, it makes for some heated debate. Let’s put it that way.

– Instead of the bible they are putting Al Gore’s book, “An Inconvenient Truth,” at the nightstand. What do you think?

– Is the debate about — I mean, we have gone up — what is it — .7 degrees?

– So there is no denying it’s happened. But I think the cause and how we can help is something that is up for debate.

Watch a compilation of the segment:

http://thinkprogress.org/2007/05/03/beck-chetry/

By giving Beck a platform to spout his junk science, CNN has helped promote ongoing efforts by the Bush administration, the oil lobby, and right-wing pundits to create doubt where none exists.



I have a strong feeling Beck also doesn't believe in evolution.

Somebody here mentioned to me that the large oil companies don't benefit from carbon controls. I think they can.

If oil is kept off the market, the price goes up. Oil is kept off the market via war in Iraq and instability elsewhere. Who benefits? Certainly the House of Saud. Also, look at the oil company profits these days. They are quite high.

Oil can be kept off the market by exaggerating a myth of peak oil and underestimates of reserves. Does this happen? Some certainly would argue this.

Finally, if there are huge controls on consumption via global carbon taxes, the infrastructure to extract the oil will not expand. And barrels of petroleum will, again, become pricier.

If oil is a finite natural resource (though HOW finite may be a matter of dispute), it makes far more sense to sell less of it at a higher price--rather than more of it at a lower price--each year. This extends the number of years of profitability for much longer.

The multinational energy companies and OPEC and all the Giants of this multi-trillion dollar industry are not going to go anywhere. Global warming or not, carbon tax or not, nothing is going to happen on planet Earth without their approval if not outright engineering.

Thus, anything done on a huge, multinational, centralized scale is going to empower them, since they will likely be pulling the strings in the first place.

Originally Posted by Ricercar71

Somebody here mentioned to me that the large oil companies don't benefit from carbon controls. I think they can.

If oil is kept off the market, the price goes up. Oil is kept off the market via war in Iraq and instability elsewhere. Who benefits? Certainly the House of Saud. Also, look at the oil company profits these days. They are quite high.

Oil can be kept off the market by exaggerating a myth of peak oil and underestimates of reserves. Does this happen? Some certainly would argue this.

Finally, if there are huge controls on consumption via global carbon taxes, the infrastructure to extract the oil will not expand. And barrels of petroleum will, again, become pricier.

If oil is a finite natural resource (though HOW finite may be a matter of dispute), it makes far more sense to sell less of it at a higher price--rather than more of it at a lower price--each year. This extends the number of years of profitability for much longer.

The multinational energy companies and OPEC and all the Giants of this multi-trillion dollar industry are not going to go anywhere. Global warming or not, carbon tax or not, nothing is going to happen on planet Earth without their approval if not outright engineering.

Thus, anything done on a huge, multinational, centralized scale is going to empower them, since they will likely be pulling the strings in the first place.

OPEC has us by the balls so to speak, oil prices would be significantly lower if we could break the OPEC cartel.

Originally Posted by Justin '77

The problem isn't that someone else has a mechanism which explains where the warming is coming from (which appears to be what you are looking for from the galactic topography discussion); it is that the anthropogenic CO2 explanation is far from rigidly exclusive. The models are fundamentally based on an assumption that a chaotic, mega-multi-input system can be understood on the basis of a small number of inputs over a vanishingly small time interval. Other inputs -- which both undeniably exist and are undeniably not tracked at present -- have impact, and as the last thirty-some-odd years of study of chaotic systems should have made clear by now to anyone, even small inputs can cause effects of all manner of scope.

I don't see what other mechanism has been proposed that would explain the increase in the late 20th century. There are many many inputs that might significantly vary the climatic system, but only a few whose input has changed significantly in the last half of the 20th century. Stellar topography, spiral arms, Milankovitch cycles, and solar forcing have not significantly shifted, and thus are not at all likely candidates. I for one would like to see a plausible changed factor other than greenhouse that could result in the observed changed reality.

I also distrust your characterization of climate as chaotic. Weather is chaotic. A trivial change in the initial conditions of a weather simulation can put storms in vastly different places. Climate is not chaotic. A small change in the input of climate models does not produce vastly different climates. There are tipping points, where polar ice melts, or methane is released from the tundra. That is not the same as the extreme sensitivity to slight changes you get with truly chaotic systems.

Originally Posted by Justin '77

Engineers make all sorts of boundary assumptions in their work; but those boundary assumptions are generally justified by either empirical evidence or by actually resolving the fundamental equations at least the one time to demonstrate that the assumed-out components are actually not critical at the scale of resolution and input being considered. This has not been done for the AGW hypothesis. Instead, AGW True Believers keep coming back to consensus. Which is one of those arguments which, the more times one hears it, begins to have a somewhat negative return...

There have been many models run over different time scales with different amounts of data. Many of them are based on the fundamental equations, while others are curve fitting statistical models. Some of the models are run with massive amounts of measured data.

There are limits to what one can do with scales of resolution. The finer the resolution, the more computation time you eat. I heard of one run that tied up a Cray supercomputer for almost a year. In abstract principle, the higher the resolution the better results one might expect. In practice, one increases resolution until the model reflects reality. If one increases the resolution further, one is just spending CPU cycles for nothing.

Still, whether you repeat basic simple pen and paper calculations done by the Victorians or one of the many and varied methods attempted by modern simulations, the results come out essentially the same.

I was interested in the abstracts dividing science into different structures. I might use slightly different words. One has data, which is essentially facts. If you release a weight off the top of a tower, one can record where it is at various times thereafter. It is hard to argue with data, though one can come up with more accurate instruments, and use them in new environments, under different circumstances.

One might propose a hypothesis, a pattern in the data, and come up with equations such as Newton's Laws.

One then might develop theories that describe what the equations represent. Theories might invisible fields of force, as Newton's did, or curved space, per Einstein.

With respect to CO2 and climate, we seem to agree on the data. We seem to agree on the pattern in the data, that there is a correspondence between CO2 concentration and climate. You seem to acknowledge that the models accurately reflect the data. We seem to understand the theory of how CO2 retains heat by absorbing IR radiation that would otherwise flow into space.

There has been no other combination data, hypothesis and or theory presented as an alternative explanation. Solar intensity has not changed over the last half of the 20th century. We haven't entered any solar arms, or the cone of a cosmic jet. There has been no nearby nova. Shifts in the Earth's orbit or axis have not been significant over the time period in question.

And yet, you are somehow rejecting all of it. You provide no new data, no new hypothesis, and no new theory that operates at all on the correct time scale or has data to confirm the theory is vaguely applicable.

If you could provide data, hypothesis or data, we could evaluate them. As you don't, how can we think you are operating within the framework of science?

Originally Posted by Justin '77

I guess at the end it comes down to what case exactly you expect the evidence that you offer to make for you.

Does the evidence appear to correlate CO2 levels with global temperature? At least weakly, yes. Does experimental evidence indicate that there is a mechanism whereby CO2 could act as a greenhouse gas? Yes. Does evidence indicate that human activities have dumped increasing amounts of CO2 into the atmosphere at least over the second half of the last century? Yes.

Does the accumulated evidence do more than suggest -- at best -- that human CO2-producing activity may have some warming impact on the global climate? No.

The problem isn't that someone else has a mechanism which explains where the warming is coming from (which appears to be what you are looking for from the galactic topography discussion); it is that the anthropogenic CO2 explanation is far from rigidly exclusive. The models are fundamentally based on an assumption that a chaotic, mega-multi-input system can be understood on the basis of a small number of inputs over a vanishingly small time interval. Other inputs -- which both undeniably exist and are undeniably not tracked at present -- have impact, and as the last thirty-some-odd years of study of chaotic systems should have made clear by now to anyone, even small inputs can cause effects of all manner of scope.

Engineers make all sorts of boundary assumptions in their work; but those boundary assumptions are generally justified by either empirical evidence or by actually resolving the fundamental equations at least the one time to demonstrate that the assumed-out components are actually not critical at the scale of resolution and input being considered. This has not been done for the AGW hypothesis. Instead, AGW True Believers keep coming back to consensus. Which is one of those arguments which, the more times one hears it, begins to have a somewhat negative return...

Isn't there a trigger point when the temps will shift the other way?

http://tinyurl.com/yve4xa

http://www.soton.ac.uk/mediacentre/n...v/05_204.shtml

Originally Posted by Ricercar71

Somebody here mentioned to me that the large oil companies don't benefit from carbon controls.

That was me.

If oil is kept off the market, the price goes up.

That depends on how and why it's kept off the market. If it's off the market because we've switched to other sources of energy, then its price will not go up. In fact, it will plummet, because demand will drop dramatically. Oil will still have uses as a source for plastics and chemicals, but if we're not burning oil products for fuel, most of the market will disappear and it will become very cheap indeed.

Originally Posted by Brian Rush

Is the climate a chaotic system or a linear one?

The fact that the question remains an unanswered one isn't sufficient?

(OTOH, when you've got an energy balance that includes at least a couple of feedback -- and double-feedback -- loops like cloud formation-albedo/insulation, temperature-related CO2-solubility, and the biospheric CO2-sinks being somewhat temperature-sensitive, to make an assumption of linearity seems a bit unreasonable. For goodness' sake, predator-prey relationships aren't even linear. Even the ones that only look at birth/death rates without regard to other environmental factors. And those are much simpler in terms of the modeled relations than is climate.)

Originally Posted by Ricercar71

Thus, anything done on a huge, multinational, centralized scale is going to empower them, since they will likely be pulling the strings in the first place.

That's really the key right there. Does anyone really think that the chiefs of oil companies give a rat's ass about global warming? They're in it because they see the opportunity to get on top and stay there.
Oil companies have been some of the biggest funders and patenters of alternative technologies. If the world is forced to move away from oil, that works to their benefit, too. After all, you can't claim royalties on oil or the internal combustion engine. It's a lot like how GE was a big supporter of California's mandate of fluorescent bulbs. The margins on them are way higher, and GE would get a captive market.

Originally Posted by Justin '77

The fact that the question remains an unanswered one isn't sufficient?

Who said it remained unanswered? The fact that they're able to model it at all shows that it IS a linear system.

All right, I shouldn't have expressed that as a question. Climate is NOT a chaotic system. There, much better.

Originally Posted by Justin '77

Oil companies have been some of the biggest funders and patenters of alternative technologies. If the world is forced to move away from oil, that works to their benefit, too.

Not as much as continuing to pump and sell oil would. And not all oil companies are doing what you say. The only one I know for certain is, is BP. Diversifying into other types of energy is a very good idea for an oil company right now, with both global warming and the oil peak on the horizon, but it's obviously a survival move, not anything conspiratorial. The longer they can delay any switch from oil, the better for their bottom lines. That's true even if they are positioned to survive the switch.

Originally Posted by Brian Rush

Who said it remained unanswered? The fact that they're able to model it at all shows that it IS a linear system.

??? Nonlinear systems can be modeled too. The example of predator-prey is just the very simplest one I could think of. But when you model a nonlinear system, you need to have a very good understanding of the inputs you are using and very good reasons for excluding the inputs you are not using. More or less what I said above.

(And climate is not a linear system; the models tend to be linear, but they are not climate, The models appear to work so well because they are tuned to reproduce the single known dataset from which they have been constructed.)

Originally Posted by Bob Butler 54

There are tipping points, where polar ice melts, or methane is released from the tundra. That is not the same as the extreme sensitivity to slight changes you get with truly chaotic systems.

Truly chaotic systems have seemingly quasi-stable ranges (even fractals have areas that, at certain resultions, can be approximates as circles or ellipses). The fact that there are 'tipping points' is even clearer proof of the non-linearity of climate. The fact that we don't know what, or where, those tipping points all are gives lie to those who would claim that our climate models only operate over a certain quasi-linear scale.

Still, whether you repeat basic simple pen and paper calculations done by the Victorians or one of the many and varied methods attempted by modern simulations, the results come out essentially the same.

Umm. No they don't . The recent climate models -- if they are in fact correct -- have revolutionized our understanding of the impact of CO2 on global climate. That is, they not only do not give 'basically the same results' as did their predecessors; but they give fundamentally new results (as you would expect making linear models of a chaotic system).

With regards to your demands for a counter-theory. One need not have an explanation for how the world works to observe that another's explanation is inadequate. How do you suppose all of the Grand Unifying Theorems have so far been discarded? Because someone else had a better equation to unify everything? Or because the equations proposed were themselves inadequate...

That's all I'm saying about the AGW models.

Originally Posted by Justin '77

With regards to your demands for a counter-theory. One need not have an explanation for how the world works to observe that another's explanation is inadequate. How do you suppose all of the Grand Unifying Theorems have so far been discarded? Because someone else had a better equation to unify everything? Or because the equations proposed were themselves inadequate...

That's all I'm saying about the AGW models.

Well, no, the Grand Unifying Theorems simply have not been able to match the data as well as the separate specialized theories. To replace established theories, one ought to strive to produce a better theory that more simply and / or more accurately matches the data. Neither the Grand Unifiers or the AGW skeptics have been able to do this. The Grand Unifiers are at least continuing to propose alternatives from time to time. The AGW skeptics can't seem to do even that much.

Originally Posted by Justin '77

That's really the key right there. Does anyone really think that the chiefs of oil companies give a rat's ass about global warming? They're in it because they see the opportunity to get on top and stay there.
Oil companies have been some of the biggest funders and patenters of alternative technologies. If the world is forced to move away from oil, that works to their benefit, too. After all, you can't claim royalties on oil or the internal combustion engine. It's a lot like how GE was a big supporter of California's mandate of fluorescent bulbs. The margins on them are way higher, and GE would get a captive market.

There are accusations not without evidence which shows energy companies funding the research of global warming skeptics. They fear if or when the crusade to shift the world's energy dependence off fossil fuels will occur, they will go out of business.

Originally Posted by Bob Butler 54

Well, no, the Grand Unifying Theorems simply have not been able to match the data as well as the separate specialized theories.

All what data? In testing GUT hypotheses, controlled experimentation is used. Either the particular GUT predicts the results of the experiments accurately or not. If not, that particular hypothesis is discarded.

AGW modeling is thus far without such falsifiability. It truly is just a hashing and re-hashing of an extremely small number of data sets.

To replace established theories, one ought to strive to produce a better theory that more simply and / or more accurately matches the data.

We're not talking about replacing an established theory. The AGW hypothesis can hardly be called 'established', as it has yet to even see its first experimental confirmation. You don't need to offer an alternative hypothesis to falsify another one. It suffices simply to point out that things simply aren't the way the hypothesis describes. A scientist would take that like a man and go on working up a better -- that is, in more accord with the way things are -- hypothesis; not start whining, "but so many people agree with me..."

Originally Posted by Brian Rush

That was me.



That depends on how and why it's kept off the market. If it's off the market because we've switched to other sources of energy, then its price will not go up. In fact, it will plummet, because demand will drop dramatically. Oil will still have uses as a source for plastics and chemicals, but if we're not burning oil products for fuel, most of the market will disappear and it will become very cheap indeed.

True enough.

Originally Posted by Justin '77

??? Nonlinear systems can be modeled too.

Sort of, but the models never match the reality except in general configuration and definition of parameters. You could not create a model of local weather conditions, for example, that tracks them the way current models track global warming. It's pretty amazing what can be done these days with chaos math, but we have to recognize too what can't be done.

But when you model a nonlinear system, you need to have a very good understanding of the inputs you are using and very good reasons for excluding the inputs you are not using. More or less what I said above.

Won't work even if you do. The problem with chaotic systems isn't that they are complex (some of them are actually quite simple), but that they are infinitely sensitive to determining conditions. Small changes to determining conditions -- changes so small there is no way to measure them accurately, in fact so small that quantum indeterminacy makes them unpredictable in principle -- produce huge changes in outcome. That makes them, not hard to predict, but impossible to predict.

Climate is not a chaotic, nonlinear system. It is a linear system that is very complex. It is not impossible to predict, but because it is complex, it is difficult to predict.

Originally Posted by Brian Rush

Climate is not a chaotic, nonlinear system. It is a linear system that is very complex. It is not impossible to predict, but because it is complex, it is difficult to predict.

I think we might not be clear on what 'nonlinear' means.

I'll steal liberally from my good friends at the Wiki

nonlinear systems represent systems whose behavior is not expressible as a sum of the behaviors of its descriptors. In particular, the behavior of nonlinear systems is not subject to the principle of superposition, as linear systems are. Crudely, a nonlinear system is one whose behavior is not simply the sum of its parts or their multiples. Linearity of a system allows investigators to make certain mathematical assumptions and approximations, allowing for simple computation of results. In nonlinear systems these assumptions cannot be made. Since nonlinear systems are not equal to the sum of their parts, they are often difficult (or impossible) to model, and their behavior with respect to a given variable (for example, time) is extremely difficult to predict. When modeling non-linear systems, therefore, it is common to approximate them as linear, where possible.
Some nonlinear systems are exactly solvable or integrable, while others are known to be chaotic, and thus have no simple or closed form solution. A possible example is that of freak waves. Whilst some nonlinear systems and equations of general interest have been extensively studied, the general theory is poorly understood....





Nonlinear equations and functions are of interest to physicists and mathematicians because most physical systems are inherently nonlinear in nature. Physical examples of linear systems are relatively rare. Nonlinear equations are difficult to solve and give rise to interesting phenomena such as chaos. A linear equation can be described by using a linear operator. A linear equation in some unknown has the form
. In order to solve any equation, one needs to decide in what mathematical space the solution u is found. It might be that u is a real number, a vector or perhaps a function with some properties.
The solutions of linear equations can in general be described as a superposition of other solutions of the same equation. This makes linear equations particularly easy to solve.
Nonlinear equations are more complex, and much harder to understand because of their lack of simple superposed solutions. For nonlinear equations the solutions to the equations do not in general form a vector space and cannot (in general) be superposed (added together) to produce new solutions.


The differential equation of motion of a simple pendulum is non-linear:

Typically this is linearized by assuming small values of theta so that sin(theta) is approximately zero, so that

For large values of θ, or if the non-linear behavior of the pendulum is of interest, the non-linear equation may be analyzed by phase plane methods, or else through the use of elliptic integrals.



Examples of nonlinear equations

• AC power flow model
• general relativity
• the Navier-Stokes equations of fluid dynamics
• systems with solitons as solutions
• nonlinear optics
• the Earth's weather system
• balancing a robot unicycle
• Boltzmann transport equation
• Korteweg-de Vries equation
• sine-Gordon equation
• nonlinear Schrödinger equation
• Ginzburg-Landau equation
• Bellman equation for optimal policy
• Richards equation for unsaturated water flow.

Thank you, Justin. Yes, that's exactly what I'm talking about, and what you linked/posted does not describe climate. In particular:

Crudely, a nonlinear system is one whose behavior is not simply the sum of its parts or their multiples. Linearity of a system allows investigators to make certain mathematical assumptions and approximations, allowing for simple computation of results. In nonlinear systems these assumptions cannot be made. Since nonlinear systems are not equal to the sum of their parts, they are often difficult (or impossible) to model, and their behavior with respect to a given variable (for example, time) is extremely difficult to predict. When modeling non-linear systems, therefore, it is common to approximate them as linear, where possible.
Some nonlinear systems are exactly solvable or integrable, while others are known to be chaotic, and thus have no simple or closed form solution.

The models coming from the IPCC treat climate as a sum of its parts or their multiples. They accurately "predict" the climate change that has already occurred. It would not be possible to do that if climate were a chaotic system. You cannot do that for the weather, for instance. You cannot have a set of equations that will accurately "predict" the past weather from a chosen starting point. Of course, you can simply plot the past weather on a graph, based on recorded knowledge, but if you try to create a model that will replicate that graph, it's not possible.

There remains some (though increasingly little) doubt about the ability of the models to predict climate change in the future, but that isn't because climate is chaotic, it's because climate is complex, and there may be significant factors that haven't been incorporated in the models or that haven't been treated accurately.